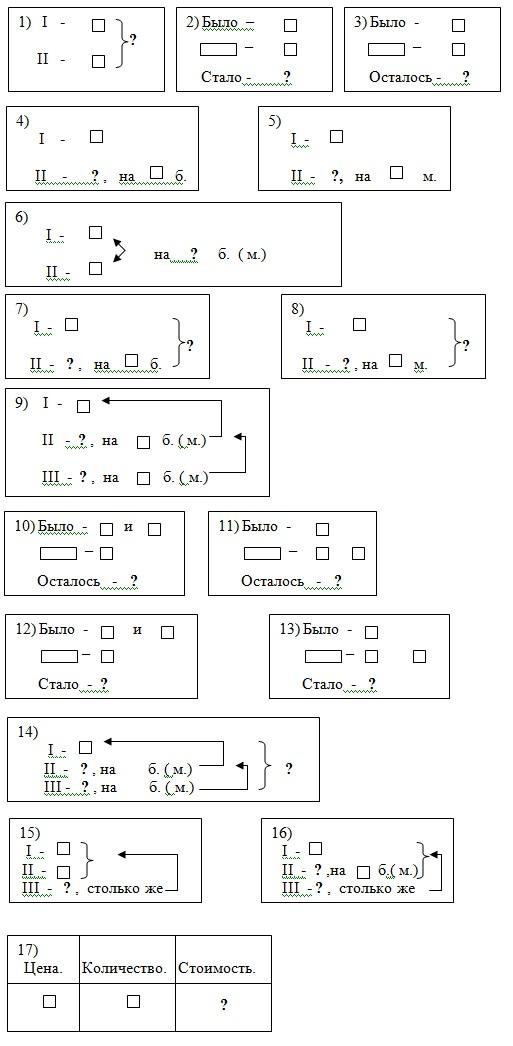
Образцы оформления задачи

Страницы

• Главная страница
• 1. Натуральные числа
• 2. Точка. Прямая. Плоскость
• 3,4 Запись натуральных чисел. Классы в записи числа
• 5. Отрезок
• 6. Сравнение натуральных чисел
• 7. Луч
• 8, 9. Координатный луч
• 10, 11 Округление натуральных чисел
• 12, 13 Сложение натуральных чисел
• 14, 15, 16. Угол
• 17. Вычитание натуральных чисел
• 18. Ломаная
• 19, 20. Задачи на нахождение чисел по их сумме и разности
• 21, 22. Множества
• 23, 24, 25. Уравнения
• 26, 28. Обобщение по теме «Сложение и вычитание натуральных чисел»
• 29, 30, 31. Умножение натуральных чисел
• 32, 33. Степень числа с натуральным показателем
• 34, 35. Прямоугольник. Квадрат
• 36, 37, 38. Распределительный закон умножения
• 40. Деление натуральных чисел
• 41, 42. Задачи на нахождение двух чисел по их сумме и частному
• 43, 44. Задачи на нахождение чисел по их разности и частному
• 45, 46. Числовые выражения
• 47, 48, 49. Выражения с переменными
• 50, 51. Задачи на части
• 52. Обобщение по теме «Умножение и деление натуральных чисел»
• 56, 57. Делители и кратные
• 58. Признаки делимости на 2 и 4
• 59. Признаки делимости на 5 и 10
• 60, 61. Задачи на нахождение общих элементов множеств
• 62, 63. Деление с остатком
• 64, 65. Признаки делимости на 3 и на 9
• 66, 67. Прямоугольный параллелепипед. Куб
• 68, 69. Объем параллелепипеда
• 70, 71, 72. Задачи на движение
• 73, 74, 75. Задачи на движение по воде
• 76. Простые и составные числа
• 77, 78. Разложение числа на простые множители
• 79. Шкалы
• 80, 81. Измерение углов
• 82, 83. Общие делители. Взаимно простые числа
• 84, 85. Наибольший общий делитель
• 86, 87. Наименьшее общее кратное
• 88. Перпендикулярные и параллельные прямые
• 89, 90. Формулы
• 93, 94, 95. Задачи на нахождение элементов множест…
• 96, 97. Понятие дроби
• 98, 99. Дробь как частное от деления натуральных ч…
• 100. Какую часть одно число составляет от другого
• 101, 102. Нахождение части (дроби) от числа
• 103, 104. Нахождение числа по его части (дроби)
• 105, 106. Основное свойство дроби
• 107, 108. Сокращение дроби
• 109, 110. Приведение дробей к общему знаменателю
• 111, 112. Сравнение дробей
• Задания по теме «Дроби»
• 113, 114. Правильные и неправильные дроби
• 115, 116, Сложение дробей с одинаковыми знаменателями
• 117-120. Сложение дробей с разными знаменателями
• 121, 122. Законы сложения дробей
• 123, 124. Вычитание дробей с одинаковыми знаменателями
• 125, 126, 127. Вычитание дробей с разными знаменателями
• 131, 132. Умножение дробей
• 133, 134. Законы умножения дробей
• 139, 140. Деление дробей
• 141, 142, 143. Часть (дробь) от числа
• 144, 145. Задачи на совместную работу
• 146, 147, 148. Обобщение по теме «Умножение и деление дробей»
• 149, 150. Смешанные дроби
• 151, 152. Сравнение смешанных дробей
• 153, 154. Изображение дробей на координатном луче
• 155, 156. Сложение смешанных дробей
• 157, 158. Вычитание смешанных дробей
• 159, 160. Умножение и деление смешанных дробей
• 161, 162. Среднее арифметическое
• 163, 164, 165. Упражнения на все действия со смешанными дробями
• 166, 168. Обобщение «Смешанные дроби»
• 169, 170, 171. Повторение

Краткая запись в зависимости от типа задач:

Возможны вариации перечисленных вариантов краткой записи в зависимости от условия задачи. Возможна и запись в виде таблиц и рисунков.

Примеры задач:

— Витя собрал коллекцию из 18 камней и разложил на коробки поровну. Сколько камней в каждой банке?

Простая задача на деление на равные части, оформляем такие задачи в виде таблицы

В 1 коробке          Количество коробок          Всего камней    ? к.                            3 к.                                18 к.

— 8 приглашений разложили в конверты, по 2 в каждый. Сколько использовали конвертов?

В 1 конверте           Количество конвертов             Всего приглашений     2 пр.                                     ? к.                             8 пр.

— Трое друзей решили сложится поровну и купить мяч стоимостью 60 рублей. Сколько денег должен дать каждый из них?

На 1 чел. денег      Количество чел.       Всего денег  поровну                      3 чел.                    60 руб.

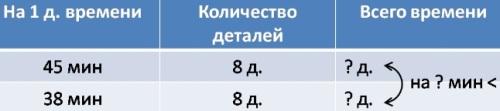
— Одну деталь мастер должен делать за 45 мин, а делает за 38 мин. Сколько времени сэкономит мастер, когда он сделает 8 деталей?

Составная задача на разностное сравнение, лучше оформить в виде таблицы.

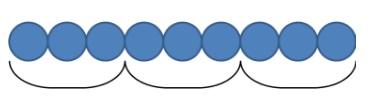
— Вера посадила 9 луковиц, по 3 луковицы в  ряд. Сколько получилось рядов?

Это простая задача на деление по содержанию. Такую задачу нагляднее оформить картинкой.

— В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось?

Задача на нахождение остатка.

Было — 20 л и 20 л Выпили — 12 л Осталось — ? л

— В куске ткани было 24 м ткани. Из 10 м этой ткани сшили одинаковые детские костюмы, а из остальной ткани-7 одинаковых детских пальто. Сколько метров ткани расходовали на одно пальто.

Было -24 м Израсходовали — 10 м Осталось — 7 к. по ? м

— Когда брат полил 5 грядок, а сестра -3 грядки, им осталось полить 4 грядки. Сколько всего грядок должны полить дети?

Было — ? гр. Полили — 5 гр. и 3 гр. Осталось — 4 гр.

— В парк привезли 33 куста роз. Когда на нескольких клумбах посадили по 6 кустов, то осталось еще 15 кустов. Сколько было клумб?

Было — 33 к. Посадили — ? кл. по 6 к. Осталось — 15 к.

— В прятки играли 12 ребят. К ним присоединились 3 девочки и 4 мальчика. Сколько всего ребят стали играть в прятки?

Было — 12 р. Пришли — 3 д. и 4 м. Стало — ? р.

— У Саши было 6 наклеек. Он подарил другу 2 наклейки. Потом Саша купил еще 5 наклеек. Сколько наклеек стало у Саши?

Было — 6 н. Подарил — 2 н. Купил — 5 н. Стало — ? н.

— На полянке паслись 14 коров, а овец на 10 больше. Сколько животных паслись на полянке?

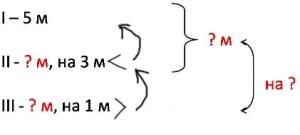
— В первый день вырыли 5м траншеи, во второй на 3м меньше, чем в первый, в третий на 1м больше, чем во второй. На сколько больше вырыли траншей в первый и во второй день вместе, чем в третий?

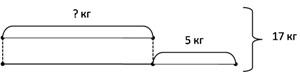
— На двух полках было 17 кг меда. Со второй полки продали 5 кг и на 2 полках стало поровну. Сколько кг меда было на 1 полке?

Нагляднее представит задачу запись в виде схемы.

Решение задач на проценты методом коэффициентов

Можно назвать еще один метод решения задач на проценты, который является следствием из формулы простого процента. Так, формулу простого процента можно переписать следующим образом:

Таким образом, мы получили формулу для решения задач на проценты методом коэффициентов. Полученная формула удобна тем, что при достаточной практике простые  задачи на проценты можно решать в уме, даже не задумываясь.

Например, яблоки стоили 150 рублей, затем они подорожали на 20%. Найдите новую стоимость яблок.

Применим полученную формулу и получим:

150 * 1,2 = 180 рублей

То есть мы интуитивно 20% превращаем в 0,2 прибавляем единицу, так как происходит увеличение на данное количество процентов, и умножаем на первоначальную стоимость.

Или другой пример. Зарплата работника составляла 25 000 рублей в месяц, в результате применения штрафа за опоздания зарплата сократилась на 10%. Найти сумму зарплаты, которую получит оштрафованный работник.

25 000 * 0,9 = 22 500 рублей

Опять же мы сразу понимаем, что 10% — это 0,1. Т.к. происходит уменьшение первоначальной величины на это количество процентов, то мы вычитаем из единицы этот процент и получаем 0,9. Затем умножаем полученное значение на первоначальную величину. Готово!

Давайте решим этим методом задачу про зарплату и налоги.

Задача 7

В России налог на доходы физических лиц составляет 13%. Зарплата Марии Ивановны после удержания налога на доходы составила 60 900 рублей. Найти сумму зарплаты Марии Ивановны до удержания налога.

Решение: Итак, 13% — это 0,13. Первоначальная зарплата уменьшилась на этот процент, значит, вычитаем из единицы и получаем 1 – 0,13 = 0,87. Подставляем в формулу:

0,87х = 60 900

х = 70 000

Ответ: 70 000 рублей

Задача 8

В школе 1000 учеников, из них 20% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучают?

Решение: Для начала из общего количества учеников исключим тех, кто французский язык точно не изучает, т.е. учеников начальной школы. Ученики начальной школы – это 20%, т.е. 0,2, мы уменьшаем на этот процент, следовательно, вычитаем из единицы и получаем 1 – 0,2 = 0,8.

1000 * 0,8 = 800

Из 800 полученных учеников французский язык изучают только 30%.

Обратите внимание, что здесь идет речь о проценте от числа. Т.е

мы не уменьшаем на 30% (в этом случае мы вычитаем значение процента в долях из единицы) и не увеличиваем на 30% (в этом случае мы прибавляем к значению процента в долях к единице), а берем 30% от заданного числа (в этом случае мы умножаем заданное число на значение процента в долях). Всегда внимательно читайте условия задачи!

В нашем случае нам нужно найти 30% от 800:

800 * 0,3 = 240

Это и есть ответ. 240 учеников изучают французский язык в школе.

Ответ: 240 учеников.

Задача 9

Разберем еще одну задачу на проценты, которая часто встречается на ЕГЭ и в которой легко можно допустить ошибку.

Задача: Зарплата рабочего составляла 30 000 рублей, затем зарплату повысили на 30%, а потом понизили на 30%. Какую зарплату стал получать рабочий?

Решение: быстро прочитав условие задачи, сходу хочется дать ответ – зарплата останется прежней, ее размер не изменился. Но это не так! Давайте разбираться.

Будем решать по формуле простого процента.

Первое событие – зарплату повысили на 30%. Следовательно, первоначальную сумму мы увеличиваем на 30%:Второе событие – зарплату понизили на 30%. Следовательно, нашу увеличенную зарплату мы теперь уменьшаем на 30%:Таким образом, рабочий теперь будет получать зарплату 27 300 рублей.

Данную задачу мы могли бы решить в одно действие, применяя формулу для вычисления сложного процента. Напомним ее:

S = P (1 + i)n, где

S – это конечная сумма;

P – это первоначальная сумма;

i – это процент/100;

n – количество периодов.

Т.к. 30% — это 0,3, то, применяя формулу для вычисления сложного процента к нашей задаче, мы получим:

30 000 * (1 + 0,3)1 (1 – 0,3)1 = 27 300 рублей

Результат получился тот же.

Ответ: 27 300 рублей

В этой статье были разобраны достаточно простые примеры задач на проценты, чтобы максимально доступно продемонстрировать методы решения задач на проценты. В профильном ЕГЭ с процентами вы можете столкнуться в задаче с экономическим содержанием по вкладам и кредитам. Такие задачи гораздо сложнее и подробное их решение вы можете посмотреть на нашем сайте.

Итак, надеюсь, что данная статья помогла вам понять, как решать задачи на проценты. Мы увидели, что задачи на проценты можно решать тремя способами – с помощью формулы простого процента, методом пропорции и методом коэффициентов. Выбирайте тот, который вам наиболее понятен, и которым вам решать такие задачи проще.

Примеры решения задач на работу: от простого к сложному

Задача 1

Первый рабочий выполняет заказ из 120 деталей на 2 часа быстрее, чем второй. Также известно, что первый рабочий делает на 3 детали в час больше, чем второй. Сколько деталей в час изготавливает первый рабочий?

Решение:

1. Составим таблицу на основании условий задачи. Производительность первого рабочего примем за Х. Тогда производительность второго рабочего будет х — 3, так как второй рабочий делает на 3 детали в час меньше первого. Время выполнения всей работы получаем путем деления всей работы на производительность.2. Также из условий задачи нам известно, что всю работу (120 деталей) первый рабочий выполняет быстрее, чем второй на 2 часа. Следовательно, получаем следующее равенство:Решаем полученное уравнение. Для этого приводим все дроби к общему знаменателю:

120 (х- 3) + 2х (х-3) = 120х

120х – 360 + 2х2 – 6х – 120х =0

2х2 – 6х – 360 = 0

Делим обе части уравнения на 2:

х2 – 3х – 180 = 0

D = 729

х₁ =  15

х₂ = -12

3. Возвращаемся к условиям задачи. Нам нужно было найти, сколько деталей изготавливает первый рабочий. Именно эту величину мы обозначали за Х. Х₂ нам не подходит по смыслу задачи. Следовательно, первый рабочий изготавливает 15 деталей в час.

Ответ: 15 деталей в час

 Задача 2 

Первая труба наполняет резервуар объемом 180 литров, а вторая труба наполняет резервуар объемом 120 литра. При этом известно, что одна из труб  пропускает на 1 литр воды в минуту меньше, чем другая. Необходимо определить, сколько литров в минуту пропускает первая труба, если резервуары наполняются одновременно.

Решение:

1. На основании условия задачи составляем таблицу. Производительность первой трубы, то есть сколько воды она пропускает в минуту, обозначим за Х. Тогда производительность второй трубы будет либо на 1 литр в минуту больше, либо на 1 литр в минуту меньше. Это мы можем обозначить, как х ± 1. Время рассчитываем по формуле и заносим в таблицу:

2. Из условий задачи нам известно, что обе трубы выполняют свою работу за одинаковое количество времени. Следовательно, время работы первой и второй трубы мы можем приравнять, тогда получим: Теперь решаем два уравнения:Решаем первое уравнение:

180/х = 120/ (х -1)

180 (х-1) = 120х

180х – 120х = 180

60х = 180

х₁ = 3

Решаем второе уравнение:

180/х = 120/ (х +1)

180 (х+1) = 120х

180х – 120х = -180

60х = -180

х₂ = -3

3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько литров в минуту пропускает первая труба. Именно это – производительность первой трубы мы и обозначали за Х. Х₂ нам не подходит по смыслу задачи. Следовательно, первая труба пропускает 3 литра в минуту.

Ответ: 3 литра в минуту

Задача 3

Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Определить сколько литров воды в минуту пропускает первая труба, если известно, что бассейн объемом 300 литров она заполняет на 3 минуты дольше, чем вторая.

Решение:

1. На основании условий задачи составляем таблицу. Производительность второй трубы обозначим за Х. Тогда производительность первой трубы Х – 5, так как она пропускает на 5 литров воды в минуту меньше. Объем бассейна (это объем работы труб) равен 300 литрам. Время работы труб определяем по формуле и заносим в таблицу:

2. Из условий задачи известно, что первая труба заполняет бассейн на три минуты дольше, чем вторая труба. Следовательно:Решаем полученное уравнение:

300х – 3х (х-5) = 300 (х — 5)

300х – 3х2 + 15х – 300х + 1500 = 0

-3х2 + 15х + 1500 = 0

Делим обе части уравнения на -3:

х2 — 5х — 500 = 0

Находим дискриминант:

D = 2025

х₁ = 25

х₂ = -20

3. Возвращаемся к условиям задачи. Нам необходимо было найти производительность первой трубы, которую мы обозначили, как (х – 5).

Подставляем полученное значение Х:

Подставляем х₁: 25 – 5 = 20

Подставляем х₂: -20 – 5 = -25

Второй результат нам не подходит по смыслу задачи. Следовательно, производительность первой трубы равна 20 литров в минуту.

Ответ: 20 литров в минуту.

Правило встречается в следующих упражнениях:

1 класс

Страница 15,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 23,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 24,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 25,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 28,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 30,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 32,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 35,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 44,
Моро, Волкова, Степанова, Учебник, 2 часть

Страница 5,
Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 63. Вариант 2. № 3,
Моро, Волкова, Проверочные работы

Страница 7,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 23,
Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 52,
Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 74,
Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 80,
Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 36,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 35. Вариант 2. № 3,
Моро, Волкова, Проверочные работы

Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 101,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 51,
Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 46,
Моро, Волкова, Рабочая тетрадь, 2 часть

4 класс

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 9,
Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 46,
Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 74,
Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 36,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 37,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

5 класс

Задание 348,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 402,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 82,
Мерзляк, Полонский, Якир, Учебник

Упражнение 164,
Мерзляк, Полонский, Якир, Учебник

Упражнение 318,
Мерзляк, Полонский, Якир, Учебник

Упражнение 367,
Мерзляк, Полонский, Якир, Учебник

Упражнение 464,
Мерзляк, Полонский, Якир, Учебник

Упражнение 481,
Мерзляк, Полонский, Якир, Учебник

Упражнение 498,
Мерзляк, Полонский, Якир, Учебник

Упражнение 508,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 365,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 366,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 372,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 409,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 419,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 420,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 432,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 437,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 447,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Любить математику, не пассовать перед ней, развивать логическое мышление- Все это можно делать, научившись решать задачи.

Как научить ребенка решать текстовые задачи? Как научить анализировать условие задачи, определять ее вид, а, значит, находить способы решения. Я предлагаю рассмотреть задачи на части и порешать их.

   Текстовые задачи в школьном курсе всегда вызывают у учащихся сложности, боязнь-а что если не получится? Ведь надо понять смысл задачи, разобрать ее условие, найти способ решения. К таким задачам относятся и задачи на части.О том, как можно рассмотреть эту тему я и хочу рассказать.

   Рассмотрим задачу.  В состав витаминного сбора входит ежевика, малина, смородина.в отношении 2:4:5. Какое количество ягод каждого вида надо взять, чтобы приготовить 264 грамма такого сбора?

   Решить эту задачу можно двумя способами.

   1 способ — по действиям.

   Витаминный сбор состоит из трех видов ягод, взятых в определенном соотношении. Найдем сначала из скольких частей состоит сбор.

1. 2+4+5=11(ч.) в витаминном сборе.

   По условию известно, что масса сбора равна 264г. Вычислим. сколько граммов ягод приходится на одну часть.

      2.  264:11=24 (г) ягод в одной части.

    А теперь осталось узнать, сколько граммов ягод в 2, 4, 5 частях, т.е сколько ягод каждого вида потребуется.

      3.  24·2=48 (г) ежевики.

      4.  24·4=96 (г) малины.

      5.  24·5=120 (г) смородины.

     Можно решить эту задачу с помощью уравнения.

     2 способ.

     Для того, чтобы решить задачу с помощью уравнения, введем неизвестное. 

     Пусть х граммов ягод в одной части, тогда 2х г ежевики, 4х г малины, 5х г смородины. По условию, масса витаминного сбора составляет 264 грамма. Составим уравнение: 2х+4х+5х=264.  Решив его, получим х=24. Значит, в одной части содержится 24 г ягод. Тогда ежевики надо взять 24·2=48 (г), малины- 24·4=96(г), а смородины- 24·5=120 (г).

      Ответ: 48 г ежевики, 96 г малины, 120 г смородины входит в 264 г витаминного сбора.

       Дальше можно провести практикум по решению задач такого вида, для этого я предлагаю следующую подборку задач.

1. В магазин привезли свеклу, морковь и картофель в отношении 7:8:12. Сколько овощей каждого вида привезли в магазин, если масса всех овощей 243 кг?
2. Сумма четерех чисел равна 156. Найдите эти числа, если их отношение равно 3:5:7.
3. Провод разрезали на две части в отношении 2:7. Найдите длину каждой части, если длина всего провода равна 54 метрам.
4. Выпуск книг в издательстве для детей представлен тремя видами детской литературы: сказками, повестями, стихами- в отношении 3:4:1. Сколько книг каждого вида выпустили в издательстве, если всего было 72 книги?
5. Как 60 конфет разделить в отношении 3:4?
6. В шахматном кружке занимаются мальчики и девочки, число которых находится в отношении 3:4. Сколько мальчиков и сколько девочек в кружке, если всего их 35?
7. Стороны треугольника относятся как 5:4:9, а периметр равен 54 см. Найдите длину каждой стороны треугольника.
8. Сумма пяти чисел равна 154. Найдите эти числа, если они относятся как 4:7:3:6:2.
9. В школу привезли красные, желтые, оранжевые мячи в отношении 3:7:11 соответственно. Сколько мячей каждого цвета привезли в школу, если всего было 168 мячей?