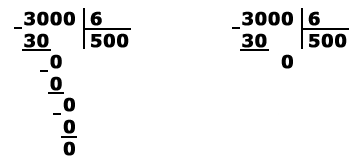Как научиться делить столбиком (уголком): примеры с решениями и объяснением

Деление различных чисел

Важно понимать, что делить можно любые числа, включая иррациональные и комплексные. Но в результате деления рациональных чисел всегда подучаются рациональные числа

В результате деления иррациональных – иррациональные и так далее.

Не может быть ситуации, когда рациональное число, делится на рациональное, а в ответе получается иррациональное число. Но может быть ситуация, когда рациональное число делится на иррациональное или наоборот. Конкретно этот момент мы и обсудим, чтобы не теряться при виде таких примеров.

В этом случае, рациональное число возводится в степень корня и вносится под знак радикала. После этого выполняется операция деления. Если из конечного результата можно извлечь корень, то операция выполняется и результатом будет рациональное число. Если корень извлечь невозможно, то результатом станет иррациональное число. Если результат обязательно нужно записать без знака радикала, то при помощи калькулятора извлекается приблизительное значение корня.

Примеры на деление трехзначного числа на двузначное с ответами:

Те же самые примеры на деление одного числа на другое, целочисленное, что приведены выше, но с ответами для быстрой проверки решений.

684 : 57 = 12396 : 36 = 11372 : 93 = 4494 : 26 = 19532 : 28 = 19520 : 20 = 26213 : 71 = 3782 : 46 = 17988 : 38 = 26575 : 23 = 25255 : 17 = 15304 : 38 = 8288 : 12 = 24441 : 21 = 21814 : 74 = 11114 : 57 = 2180 : 30 = 6168 : 12 = 14960 : 12 = 80945 : 35 = 27600 : 40 = 15220 : 20 = 11182 : 26 = 7820 : 20 = 41869 : 79 = 11770 : 10 = 77611 : 47 = 13602 : 86 = 7784 : 28 = 28779 : 41 = 19405 : 45 = 9960 : 80 = 12459 : 17 = 27130 : 26 = 5864 : 24 = 36380 : 20 = 19684 : 36 = 19990 : 30 = 33744 : 24 = 31793 : 61 = 13816 : 17 = 48896 : 56 = 16806 : 26 = 31114 : 38 = 3957 : 87 = 11485 : 97 = 5648 : 24 = 27901 : 53 = 17216 : 36 = 6585 : 15 = 39915 : 61 = 15495 : 11 = 45897 : 23 = 39480 : 60 = 8732 : 61 = 12961 : 31 = 31645 : 43 = 15900 : 12 = 75720 : 15 = 48992 : 31 = 32918 : 54 = 17527 : 17 = 31442 : 17 = 26235 : 47 = 5720 : 90 = 8980 : 14 = 70602 : 14 = 43140 : 70 = 2405 : 81 = 5552 : 23 = 24873 : 97 = 9180 : 18 = 10504 : 42 = 12236 : 59 = 4902 : 41 = 22238 : 34 = 7364 : 52 = 7966 : 42 = 23735 : 15 = 49451 : 41 = 11940 : 20 = 47150 : 75 = 2830 : 10 = 83703 : 19 = 37252 : 84 = 3558 : 18 = 31720 : 80 = 9455 : 35 = 13759 : 23 = 33468 : 18 = 26730 : 10 = 73832 : 16 = 52850 : 17 = 50320 : 16 = 20760 : 38 = 20782 : 23 = 34986 : 58 = 17590 : 59 = 10280 : 14 = 20216 : 54 = 4

693 : 99 = 7855 : 19 = 45782 : 17 = 46261 : 87 = 3624 : 52 = 12693 : 33 = 21553 : 79 = 7172 : 86 = 2198 : 99 = 2960 : 32 = 30531 : 59 = 9336 : 84 = 4610 : 10 = 61336 : 24 = 14621 : 23 = 27396 : 11 = 36551 : 29 = 19832 : 26 = 32860 : 20 = 43928 : 58 = 16720 : 20 = 36868 : 14 = 62432 : 54 = 8120 : 20 = 6399 : 21 = 19792 : 22 = 36648 : 18 = 36640 : 16 = 40481 : 37 = 13189 : 63 = 3949 : 13 = 73924 : 14 = 66473 : 11 = 43840 : 21 = 40240 : 16 = 15836 : 76 = 11740 : 37 = 20576 : 32 = 18640 : 32 = 20304 : 16 = 19285 : 15 = 19363 : 11 = 33462 : 66 = 7962 : 13 = 74456 : 38 = 12810 : 18 = 45999 : 37 = 27845 : 65 = 13600 : 75 = 8273 : 21 = 13480 : 16 = 30462 : 42 = 11609 : 29 = 21960 : 24 = 40168 : 42 = 4288 : 16 = 18432 : 36 = 12300 : 10 = 30820 : 10 = 82258 : 43 = 6460 : 23 = 20682 : 31 = 22810 : 27 = 30931 : 19 = 49988 : 19 = 52646 : 19 = 34664 : 83 = 8640 : 64 = 10621 : 69 = 9470 : 94 = 5403 : 31 = 13266 : 19 = 14540 : 45 = 12722 : 38 = 19891 : 27 = 33190 : 95 = 2588 : 12 = 49498 : 83 = 6765 : 15 = 51987 : 47 = 21360 : 18 = 20420 : 12 = 35828 : 12 = 69832 : 52 = 16112 : 56 = 2220 : 44 = 5198 : 33 = 6308 : 22 = 14832 : 32 = 26736 : 32 = 23580 : 20 = 29833 : 49 = 17950 : 38 = 25880 : 40 = 22448 : 32 = 14570 : 38 = 15752 : 94 = 8940 : 10 = 94902 : 22 = 41148 : 74 = 2

Сгенерировано примеров на деление трехзначного числа на двузначное с ответами в качестве тренажера по математике: 200

Скачать

Распечатать

На этой странице сайта результат работы генератора случайных примеров по математике на деление трехзначного числа на двузначное для тренировки арифметических действий учениками 1, 2, 3, 4 классов средней общеобразовательной школы.

Тренировочные примеры по математике на деление трехзначного числа на двузначное для учеников первого, второго, третьего, четвертого класса можно отображать для распечатки или скачивания в два, три или четыре столбца.

Математические примеры на деление трехзначного числа на двузначное, которые приведены на этой странице сайте, могут использоваться в качестве тренажера для отработки арифметических действий учителями, преподавателями, родителями или репетиторами для учащихся 1-го, 2-го, 3-го, 4-го класса.

Задания на деление трехзначного числа на двузначное, которые находятся в этом разделе сайта, можно использовать в карточках на уроках математики для закрепления пройденного материала.

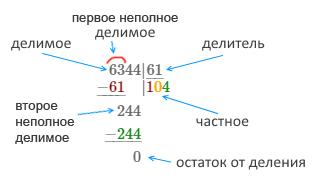
Как правильно делить числа в столбик: алгоритм деления

алгоритм деления чисел столбиком

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

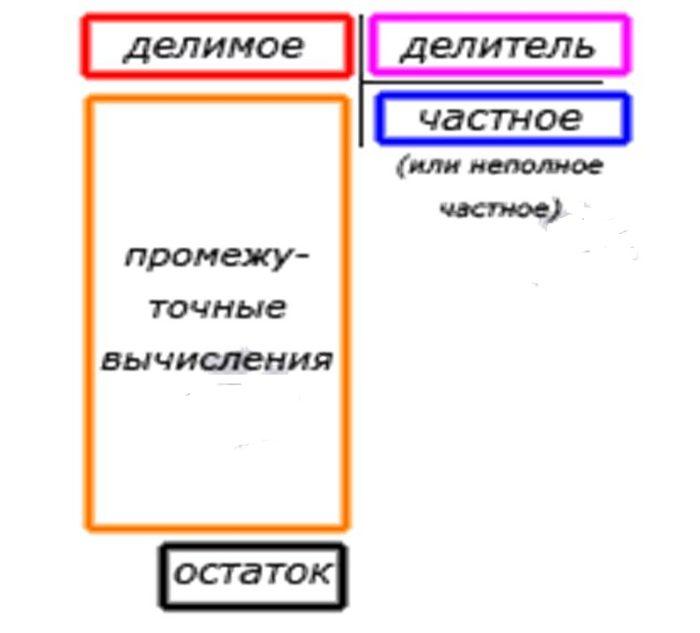
схема и назнвания составных элементв действия деления чисел столбиком

• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Деление трехзначного числа на однозначное

Такие операции, как правило, выполняют в столбик для простоты расчета. Рассмотрим пример деления трехзначного числа на однозначное: 967 поделим на 23.

Столбик это вертикальная линия, к середине которой проводится горизонтальная. Над горизонтальной чертой пишется делитель, с другой стороны вертикальной черты, рядом с делителем записывают делимое. Под горизонтальной чертой будет записываться результат.

Первым этапом нужно среди первых цифр числа 967 найти число, которое больше 23. Рассматриваем по порядку: 9 – меньше 23, а вот 96 уже больше. Значит первым шагом мы делим число 96 на число 23. Обязательно с остатком.

96:23=8, ост. 4 – в столбике под 96 записывается результат произведения 8*23=92. Число 92 подчеркивается и под ним записывается результат разности: 96-92=4. Рядом с 4 сносится цифра 7. Получается число 47, которое таким же образом делится на 23. А число 8 будет первой цифрой в результате.

47:23=2, ост. 1 – цифра 2 будет второй цифрой результата.

Рядом с 1 можно снести 0 и считать уже дробную часть частного, но мы поделим число с остатком.

Результат: 967:23=82, ост.

Что мы узнали?

Мы узнали, что такое деление, поговорили о свойствах деления и отдельно обсудили деление трехзначного числа на однозначное. Привели небольшой пример подобного деления в столбик с остатком.

Как делить столбиком числа с нулями?

улыбчивая девочка у школьной доски

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Деление с остатком

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета.
• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.
• «Ищем дерево». Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой.

Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком.

Если педагогического опыта у вас нет, посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом. Этот вариант оставим на крайний случай.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.

2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Вычитание трёхзначных чисел | Теория

А) Если каждая из цифр вычитаемого числа меньше соответствующей цифры числа, из которого производится вычитание, то задачу удобно решать простым вычитанием «слева направо» (сначала отнимите сотни, затем десятки, и, наконец, единицы). Эта методика может применяться для всех случаев вычитания двузначных чисел, но, как будет показано дальше, в сложных случаях более эффективной может оказаться другая методика.

Задача: 784 – 342

Решение:

748 – 342(300+40+2) = 748 – 300 – 40 – 2

748 – 300 = 448; 448 – 40 = 408; 408 – 2 = 406

Такую задачу также удобно решать вычитанием соответствующих цифр двух чисел.

748 – 342 = (7-3)(4-4)(8-2) = 406

Б) Если в вычитаемом числе имеются цифры, которые больше соответствующих цифр числа, из которого производится вычитание, то задача усложняется, но и в этом случае имеется удобной способ быстрого решения такой задачи в уме с помощью метода «дополнения»:

1) округлите вычитаемое число в большую сторону до сотен;

2) отнимите округлённое число;

3) определите «дополнение» (см. ниже);

4) прибавьте к результату пункта 2 «дополнение».

Разница между округлённым числом и вычитаемым числом называется «дополнением».

Допустим, вычитаемое число равно 487. Округляя вычитаемое число в большую сторону до сотен, получаем число 500. «Дополнение» равно: 500 – 487 или, если проще: 100 – 87 (487 меньше 500 настолько, насколько 87 меньше 100).

Таким образом, «дополнение» легче представить как число, которое нужно прибавить к десяткам и единицам вычитаемого числа, чтобы в сумме получить 100.

Для вычисления в уме «дополнения» двузначного числа наиболее эффективна следующая методика*:

1) определите, какую цифру нужно прибавить к первой цифре числа, чтобы получить в сумме 9 (если число не заканчивается на 0) или 10 (если число заканчивается на 0);

2) определите, какую цифру нужно прибавить ко второй цифре числа, чтобы получить в сумме 10 (если число не заканчивается на 0); если число заканчивается на ноль, то искомая цифра также будет 0;

3) соединив найденные цифры, получите величину «дополнения».

Задача: найти дополнение числа 87

Решение:

8 + 1 = 9

7 + 3 = 10

13

С помощью метода «дополнения» решим задачу: 632 – 487

Решение:

1) округление 487 в большую сторону до сотен даёт 500;

2) отнимаем округлённое число: 632 — 500 = 132;

3) как было вычислено выше, «дополнение» равно 13;

4) прибавляем к результату пункта 2) дополнение: 132 + 13 = 132 + 10 + 3; 132 + 10 = 142; 142 + 3 = 145.

Решим ещё одну задачу: 841 — 268

Решение:

В вычитаемом числе имеются цифры, которые больше соответствующих цифр числа, из которого производится вычитание. Поэтому решим задачу с помощью метода «дополнения».

1) округление 268 в большую сторону до сотен даёт 300

2) отнимаем округлённое число: 841 — 300 = 541

3) определяем «дополнение»: 6 + 3 = 9; 8 + 2 = 10; 32

4) прибавляем к результату пункта 2) дополнение: 541 + 32 = 541 + 30 + 2; 541 + 30 = 571; 571 + 2 = 573.

* Математическое обоснование методики определения «дополнения» двузначного числа:

Допустим, имеется двузначное число ХY, первый знак которого — X, а второй – Y.

Если двузначное число, к которому определяется дополнение, не заканчивается на 0:

—	100
XY
	(10-1-X)(10-Y)

Согласно правилам вычитания столбиком, если Y больше 0 (Y равен любой цифре, кроме 0), то из разряда десятков отнимается единичка.

Если двузначное число, к которому определяется дополнение, заканчивается на 0:

—	100
X0
	(10-X)0

Алгоритм деления столбиком на двузначное число

1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака. 

           Примеры        768:24. Первое неполное делимое 76                                265:53  26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.

2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.

           Примеры       768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.                                265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.                               15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.

3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.

Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.

4. Находим остаток (если есть).

Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.

Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)