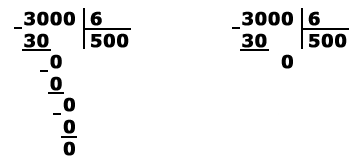3 класс: деление с остатком, примеры и пояснения

Что нужно для освоения деления в младшем школьном возрасте

Деление — это не первое арифметическое действие, которое осваивают дети. Поэтому, прежде чем браться за «делимое-делитель-частное», нужно обязательно выяснить, знает ли ребёнок разряды чисел и понимает ли принципы:

• сложения;
• вычитания;
• умножения.

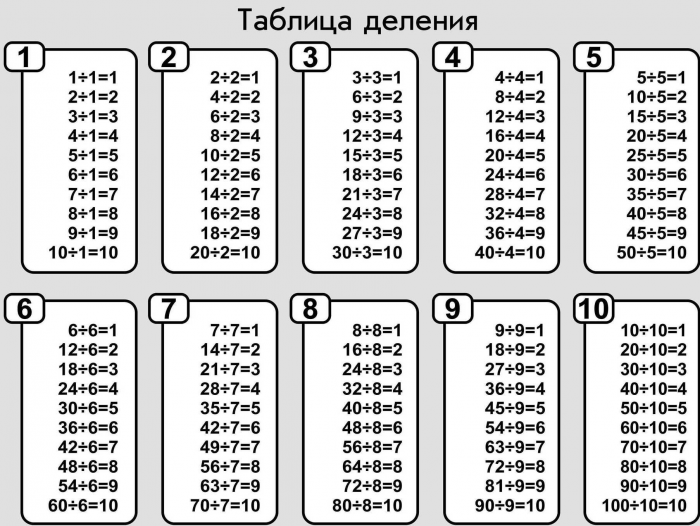
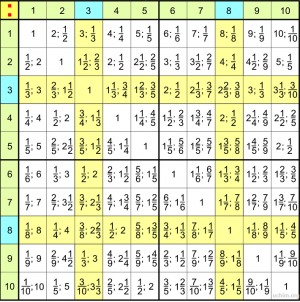
Таблицей деления дети могут проверять решения примеров

Эффективные способы объяснения деления школьникам

Все способы объяснения можно условно поделить на академичные и образные. Первые опираются на цифры, то есть записываются в виде арифметических примеров, вторые — на конкретные предметы: конфеты, мячи и т. д., которые умозрительно делятся между людьми, игрушками.

В работе с учениками начальной школы эффективным будет синтетический способ, совмещающий опору на образы и цифры одновременно.

Деление на основе знания таблицы умножения

Для понимания сути деления стоит обратиться к вычислениям с опорой на таблицу умножения.

Инструкция:

1. Записываем пример: 2 х 5 = 10.
2. Берём 10 монет и просим поделить их на двоих — получается две стопки по 5 монет.
3. Далее 10 монет делим на пятерых — получается 5 стопок по 2 монеты.
4. Вывод — при делении мы выясняем, сколько раз каждый множитель помещается в произведении.

На этом приёме разъясняем понятийную базу: то число, которое делится, называется делимое, то число, на которое делится — делителем, а результат — частным.

Поскольку деление обратно умножению, то второе может проверить результат первого.

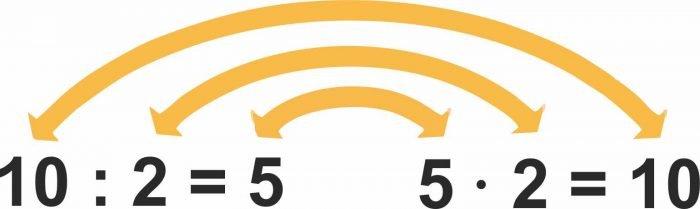
Первое время для закрепления навыка можно зарисовывать схему перестановки значений при делении и при проверки умножением

Инструкция:

1. Делимое делим на делитель, то есть 10 : 2.
2. Получаем частное — 5.
3. Проверяем умножением, то есть частное умножаем на делитель — 5 х 2.
4. Получаем 10, что в исходном примере является делимым.

Деление двузначных чисел на однозначные

Чтобы разделить двузначное число, не являющееся произведением таблицы умножения, на однозначное, нужно каждую цифру делимого разделить на делитель и записать первое частное десятками, а второе — единицами. Например, 86 : 2.

Инструкция:

1. Делим 8 на 2. Получаем 4.
2. Делим 6 на 2. Получаем 3.
3. Ответ — 43.
4. Проверяем — 43 х 2 = 86.

Деление способом группирования

Суть этого способа деления заключается в подсчёте количества групп равных делителю, которые помещаются в делимое. Результат будет частным.

Инструкция:

1. Задача состоит в распределении мячей между командами. Решаем пример — 30 : 3.

2. Распределим 30 мячей между тремя командами — обводим тройки.
3. Считаем количество групп троек — 10. Каждой команде достанется по 10 мячей.
4. Вывод — 30 : 3 = 10.

Как объяснить деление в столбик

Поскольку деление может быть без остатка, а может быть с остатком, рассмотрим два варианта объяснение такого арифметического действия.

Деление без остатка

Инструкция:

1. Решим пример 396 : 3.

2. Записываем делимое, справа рисуем повёрнутую на левый бок букву Т и в верхнем «окошке» вписываем делитель — 3.
3. Начинаем с сотен. 3 делится на 3 без остатка, получаем 1. Вписываем результат под делителем.
4. Проверяем — 1 х 3 получаем 3, вписываем 3 под сотней и производим вычитание. Остатка нет. Подводим черту.
5. Приступаем к десяткам. 9 : 3 получаем 3. Записываем 3 рядом с 1.
6. Проверяем — 3 х 3 получаем 9, вписываем 9 под чертой, производим вычитание. Остатка нет. Подводим черту.
7. Работаем с единицами. 6 : 3 получаем 2. Записываем 2 рядом с 13.
8. Проверяем — 2 х 3 получаем 6, вписываем 6 под чертой, вычитаем. Остатка нет.
9. Результат — 132.

Деление с остатком

Инструкция:

1. Решим пример 90 : 4.

2. В десятках помещается две четвёрки. В частном запишем значение 2, затем перемножаем 2 х 4 = 8, вписываем под 9 полученное произведение, вычитаем и получаем 1.
3. Сносим к разности 0, получаем 10. В 10 помещается 2 четвёрки, 10 — 8 = 2. Это остаток.
4. 2 на 4 не делится. Ставим десятичную запятую в частном и добавляем 0 к 2.
5. 20 : 4 = 5. Записываем частное после запятой.
6. Проверяем умножением — 5 х 4 = 20. 20 — 20 = 0 — остатка нет.

Деление на двузначные числа

Если в делителе есть десятки, сотни, то для облегчения решения делитель можно упростить, разбив на единицы (десятки).

Для деления на десятки нужно воспользоваться правилом упрощения

Инструкция:

1. Решим пример — 405 : 15.
2. Разобьём 15 на единицы, на 5 и 3 — их произведение равно 15.
3. Теперь решаем два примера. Сначала 405 : 5. Частное 81.
4. Затем 81 : 3. Частное 27.
5. Результат — 405 : 15 = 27.

Видео: тренажёр быстрого деления в уме для школьников

Объяснить деление можно не только школьнику, но и дошкольнику. Причём не только в условиях детского сада, школы, но и дома. Для этого нужно убедиться, что ребёнок имеет опорные знания, и у родителя есть запас времени, терпения для регулярных занятий со своим чадом.

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

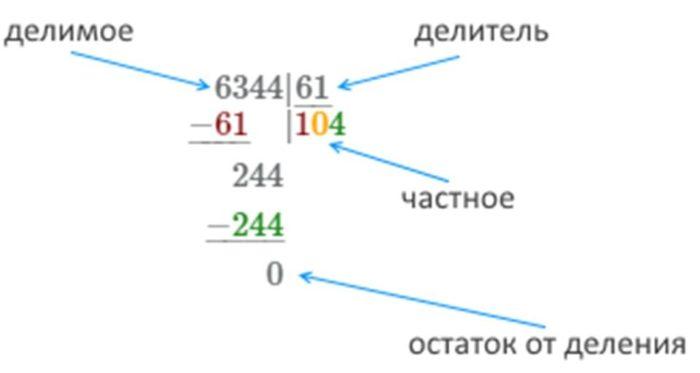
пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

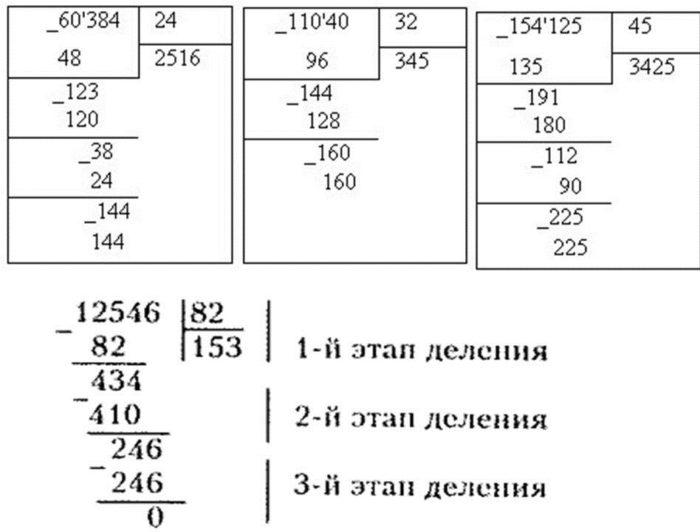
примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Остаток от деления

Остаток всегда должен быть меньше делителя.

Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.

Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.

Вопросы по теме “Деление с остатком”:Остаток может быть больше делителя?
Ответ: нет.

Остаток может быть равен делителю?
Ответ: нет.

Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)

Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8

Решение:
а) Делим столбиком:

258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.

Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258

б) Делим столбиком: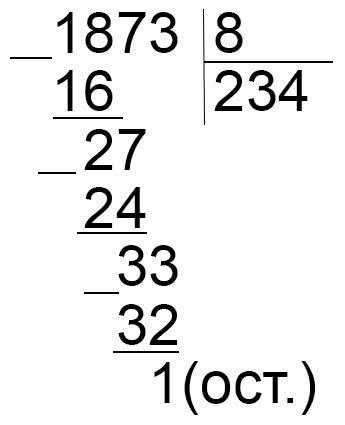

1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.

Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873

Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.

Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.

Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)

Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22

б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107

Задача:

Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?

Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400

Ответ: 30 кусков получиться и 10 см. проволоки останется.

Признаки делимости

Для выполнения деления с остатком в столбик нужно знать о признаках делимости. Это правила, помогающие производить операцию без ошибок. К ним относятся (порядковый номер соответствует делителю):

1. Можно делить любое действительное число. Результат операции — первоначальное значение.
2. Четный разряд единиц.
3. Сумму разрядов можно поделить на тройку.
4. Две цифры, являющиеся последними, можно разделить на четверку.
5. Последний разряд заканчивается на 0 или 5.
6. Одновременное деление по второму и третьему пунктам.
7. Произведение всех разрядов, кроме первого, без удвоенной последней цифры делится на семерку, то есть для числа 123 формула записывается в таком виде: (1*2−2*3)/7=-8/7 (не делится).
8. Для последней группы, состоящей из трех разрядов, выполняются условия пунктов 2 и 4.
9. Деление суммы всех разрядов на 9.

Операция «mod» и связь со сравнениями

Величина остатка может быть получена бинарной операцией «взятия остатка» от деления a{\displaystyle a} на b{\displaystyle b}, обозначаемой mod:

r=a  mod  b.{\displaystyle r=a~~{\bmod {~}}~b.}

Не следует путать это обозначение с обозначением сравнения по модулю b{\displaystyle b}. Формула для r{\displaystyle r} влечёт выполнение сравнения:

r≡a(modb),{\displaystyle r\equiv a{\pmod {b}},}

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства ⩽r<|b|{\displaystyle 0\leqslant r<|b|}, необходимого для того, чтобы r{\displaystyle r} было остатком.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Алгоритм деления столбиком

Методика включает в себя деление с остатком и проверку результата посредством операции умножения. Для ее выполнения требуется указать делимое, а затем справа записать делитель, отделяя его от первого. Рекомендуется также отделять делитель от результата.

Допустим, число 793 нужно разделить на 3. Это рекомендуется делать по такому алгоритму:

1. Проверка делимости нацело: 7+9+3=19 (не делится).
2. Записать значения 793 и 3, разделив их чертой.
3. Отделить первое неполное делимое, подобрать близлежащее на числовой прямой целое: 7=2*3+1.
4. Величину 2 внести поле результата, а затем умножить его на делитель: 2*3=6.
5. Сравнить первый элемент и значение, полученное в четвертом пункте: 7>6 (условие выполняется).
6. Записать остаток 1 под 7.
7. Перенести второй элемент трехзначного числа: 19.
8. Выполнить подбор ближайшего целого для значения, полученного в седьмом пункте: 19=3*6+1.
9. Проверить истинность неравенства: 19>18 (истинно).
10. Осуществить запись второй цифры результата: 26.
11. Перемножить делитель на подобранное значение, записав его под 19: 3*6=18.
12. Выполнить операцию разности 19 и величины, полученной в десятом пункте: 19−18=1.
13. Осуществить перенос третьего разряда: 13.
14. Решить неравенство с учетом целочисленного результата: 13<3t. t<5.
15. Ближайшее целое — 4, поскольку 3*5=15>13 (ложное неравенство).
16. Записать величину 4 в поле результата: 264.
17. Произведение делителя на 4: 4*3=12<13 (подходит).
18. Записать 12 под 13, а затем получить остаток, вычитая в этом случае из второго первое значение: 13−12=1.
19. Окончательный результат: 264 (+1).
20. Проверка может делаться при помощи калькулятора или ручным способом в столбик. При этом остаток учитывать не нужно, а следует брать 264 и умножать его на 3: 264*3=792.

В последнем пункте алгоритма получилось значение 792, а с учетом остатка вышла искомая величина, то есть 792+1=793. Умножение в столбик осуществляется по такой методике:

1. Умножается разряд единиц на 3: 4*3=12.
2. Двойка остается, а 1 записывается над 6.
3. Перемножаются 6 и 3, затем прибавляется к полученному произведению величина во 2 пункте: 6*3+1=19 (9 остается, а 1 идет в сотни).
4. Умножение множителя 3 на разряд сотен с учетом 1 (3 пункт): 3*2+1=7.
5. Искомый результат: 792.

Таким образом, для выполнения деления с остатком в столбик необходимо знать признаки делимости чисел и описанный алгоритм с проверкой.

Пример с умножением

Одна из самых трудных тем, с которой сталкивается 3 класс, — деление с остатком. Примеры могут быть сложными, особенно когда требуются дополнительные расчеты, записываемые в столбик.

Допустим, необходимо разделить число 190 на 27 с получением минимального остатка. Попробуем решить задачу, пользуясь умножением.

Подберем число, которое при умножении будет давать цифру, максимально приближенную к числу 190. Если умножить 27 на 6, получим цифру 162. Вычтем из 190 число 162, остаток будет 28. Он получился больше, чем исходный делитель. Следовательно, число шесть не подходит для нашего примера в качестве множителя. Продолжим решение примера, взяв для умножения число 7.

Умножая 27 на 7, мы получим произведение 189. Далее проведем проверку правильности решения, для этого вычтем из 190 полученный результат, то есть отнимем число 189. Остатком будет 1, что явно меньше 27. Именно так решаются сложные выражения в школе (3 класс, деление с остатком). Примеры всегда предусматривают запись ответа. Все математическое выражение можно оформить так: 190:27=7 (остаток 1). Подобные вычисления можно производить и в столбик.

Именно так осуществляет 3 класс деление с остатком. Примеры, приведенные выше, помогут разобраться в алгоритме решения подобных задач.

Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.

Как делить в столбик лучше всего объяснить на примере. Вычислить

512:8=?

Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:

Их частное (результат) будем записывать под делителем. У нас это цифра 8.

     1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.

     2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя). 

После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.

     3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:

Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).

Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения

     4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.

Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). 

В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.

Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.      5

Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается

     5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.

Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:

В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2) ).

В программировании

Операция вычисления неполного частного и остатка в различных языках программирования

Язык	Неполноечастное	Остаток	Знак остатка
ActionScript			Делимое
Ada			Делитель
	Делимое
Бейсик			Не определено
Си (ISO 1990)		Не определено
Си (ISO 1999)		Делимое
C++ (ISO 2003)		Не определено
C++ (ISO 2011)		Делимое
C#		Делимое
ColdFusion			Делимое
Common Lisp			Делитель
		Делимое
D		Делимое
Delphi			Делимое
Eiffel			Делимое
Erlang			Делимое
Euphoria			Делимое
Microsoft Excel (англ.)			Делитель
Microsoft Excel (рус.)
FileMaker			Делитель
Fortran			Делимое
		Делитель
GML (Game Maker)			Делимое
Go		Делимое
Haskell			Делитель
		Делимое
J			Делитель
Java		Делимое
		Делитель (1.8+)
JavaScript	.toFixed(0)		Делимое
Lua			Делитель
Mathematica			Делитель
MATLAB			Делитель
		Делимое
MySQL			Делимое
Oberon			+, если делитель >0
Objective Caml			Не определено
Pascal			Делимое
Perl	Нет		Делитель
PHP	Нет		Делимое
PL/I			Делитель (ANSI PL/I)
Prolog (ISO 1995)			Делитель
PureBasic		Делимое
Python			Делитель
QBasic			Делимое
R			Делитель
RPG			Делимое
Ruby		Делитель
Scheme			Делитель
SenseTalk			Делитель
	Делимое
Tcl			Делитель
Verilog (2001)			Делимое
VHDL			Делитель
	Делимое
Visual Basic			Делимое

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция вычисляет остаток от деления, а операция осуществляет целочисленное деление, при котором остаток от деления отбрасывается:

78 mod 33 = 12
78 div 33 = 2

Знак остатка

Важно отметить, что операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

• Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
• Знак остатка совпадает со знаком делителя: неполное частное округляет к −∞{\displaystyle -\infty }, соответствует определению из начала статьи.

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

• Есть сумма n копеек, положительная или отрицательная. Перевести её в рубли и копейки: и . Знак остатка совпадает со знаком делимого.
• Есть бесконечное клеточное поле, каждая клетка 16×16 пикселей. В какую клетку попадает точка (x, y), и каковы координаты относительно верхнего левого угла клетки? Ответ: и соответственно. Знак остатка совпадает со знаком делителя.

Как запрограммировать, если такой операции нет?

Неполное частное можно вычислить через деление и взятие целой части: q=ab{\displaystyle q=\left}, где x{\displaystyle }, в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды остаток программируется как a−qb{\displaystyle a-qb}.

Если b{\displaystyle b} положительно, а знак r{\displaystyle r} совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой r′=(b+(amod⁡b))mod⁡b{\displaystyle r’=(b+(a\operatorname {mod} b))\operatorname {mod} b}.

Неполное частное и неотрицательный остаток от деления на степень двойки 2n{\displaystyle 2^{n}} — это битовый сдвиг a≫n{\displaystyle a\gg n} (для чисел со знаком — арифметический) и a&⁡(2n−1){\displaystyle a\mathop {\&} (2^{n}-1)}.

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу

В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет:

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.