Сложение и вычитание двузначных чисел

Система счисления

Для начала решим, какие числа в математики считаются двузначными. По слову сразу ясно, что это числа, которые содержат два значащих знака. Значащие позиции считаются от единиц вверх, по есть по готовому числу справа налево.

Сначала идут единицы, затем десятки, сотни и так далее. При этом знаки могут распространяться и +влево от единиц в виде десятичных дробей после запятой.

Такая система называется позиционной. Каждая цифра в ней меняет свое значение в зависимости от занимаемой позиции. Например, есть число 23, а есть 32 и это разные числа, которые были записаны при помощи одинаковых цифр. Благодаря такому подходу можно записать любое по своей величине число с помощью всего 9 цифр от 1 до 0.

Отдельно стоит сказать, что значащей считается любая позиция, отличная от нуля. В любом числе незначащих позиций бесконечно много. Мы пишем 23, но понимаем, что в этом числе 0 сотен и тысяч, то есть можно записать его, как 0023.

Сложение и вычитание двузначных чисел с переходом через разряд

Сложность выполнения действий заключается в том, что нужно будет «запоминать» числа при сложении и «занимать» при вычитании.

Сначала пример решают с помощью палочек (например, 25+37):

1. Выкладывают числа палочками, складывают разрядные единицы. Получается 5 горизонтальных и 12 вертикальных палочек.
2. Вспоминают, что 10 единиц – это десяток, поэтому их можно заменить одной горизонтальной палочкой.
3. Получается 6 десятков и 2 единицы. Значит, 25+37=62.
4. Делают вывод: при сложении единиц получилось число больше 10, поэтому разделили его на десяток и единицы, а затем определили число. Удобнее сначала складывать единицы (если их будет больше десяти, то можно без особых проблем выделить десяток и добавить его к имеющимся).

После наглядного примера рассматривают сложение в столбик и другие способы складывания двузначных чисел:

• Сначала к числу прибавляют десятки, а потом единицы: 25+37=(25+30)+7=62;
• Первое слагаемое доводят до круглого (25+5=30), потом к нему прибавляют второе (30+37=67) и отнимают столько, сколько добавляли в первом действии (67-5=62);
• Отдельно складываются единицы, отдельно – десятки, а потом – результаты: 25+37=(20+30)+(5+7)=50+12=62.

Суть вычитания с переходом разряд также желательно сначала показать наглядно (например, 42-15):

1. Выкладывают первое число (4 десятка и 2 единицы).
2. Определяют, что из 2 единиц нельзя вычесть 5, поэтому один десяток нужно «перевести» в единицы (заменить десятью вертикальными палочками).
3. Дальнейшие действия: из 12 единиц вычитают 5, получается 7, далее отнимают десятки (желательно проговорить, что было 4, а после преобразования осталось 3).
4. В итоге получается 2 десятка и 7 единиц, или 27. Проверить вычитание нужно с помощью сложения, чтобы убедиться, что решили пример правильно.

После наглядного метода рассматривается вычитание в столбик и несколько других способов:

• Сначала вычитают десятки, потом – единицы: 42-15=42-10-5=27;
• Наоборот, сначала – единицы, потом – десятки: 42-15=42-5-10=37-10=27.

Для объяснения арифметических действий можно использовать счеты. На них для каждого разряда имеется свое место, поэтому детям будет несложно «записывать» на них числа, а затем производить действия.

Любой метод может быть успешным только в том случае, если его подбирать в соответствии с особенностями ребенка. Ведь одним достаточно объяснить принцип сложения и вычитания с помощью цифр, другие не поймут до тех пор, пока сами не «увидят» решения.

И, конечно, немаловажную роль в освоении любого материала играет систематизация: работать с примерами нужно регулярно в необходимом объеме.

Учим детей математике сами. Часть 2 «Сложение и вычитание двухзначных чисел.»

Продолжение. Начало здесь: Учим детей математике сами. Часть 1 «Знакомство»Традиционно А зачем всё это? А какой в этом толк?

Сын в 4 года научился САМ находить закономерности десятичной системы. Что девятка отнимает от числа при сложении 1. То есть 11+9=20.Что 13+14 проще сосчитать как 3+4=7, а потом +10 и +10 и = 27 ! И всё в уме.Как я узнал, что он именно так думает? Так я же слышу, что он говорит. И я знаю, как считаю я сам, помню из собственного детства, как овладевал цифрами, правда, мне было лет 8 уже. И это то же самое! Я натурально узнаю тот же ход мыслей.

СчётыОчень полезным для нас оказалось освоение счёт. В сети легко найти алгоритм пользования ими.Сложнее было найти нормальные счёты. Купили в икее.Я фломастером раскрасил пятую и шестую костяшки в каждом ряду, чтоб они отличались. Так удобней. Сын понемножку начал отходить от пересчитывания точек на доске к оперированию числами в уме.

Сложение двузначных чиселСнова использовал Excel, чтоб сделать листики с заданиями:Сюда же сунул и вычитание. И специально сделал пропуски на месте уменьшаемого и вычитаемого. Сын стал интуитивно ориентироваться в примере. Потом будет проще решать уравнения.

СтолбикомПростой пример 25+64=89, когда числа в каждом столбике не выходят за пределы десятки. С таких начинали.Сложый пример 74-36=38, когда приходится «занимать» и «держать в уме».Сын долго не понимал, как числа складываются и особенно вычитаются столбиком. Путался. На две недели мы сделали перерым в математике. Когда вернулись, всё стало само получаться. «Надо давать паузу, – как говорил Жванецкий, – а то до народа не доходит».

Вот думаю: нас научили в детстве складывать числа до десяти в уме. Двузначные не требуют в уме – можно столбиком. Трёхзначные и больше – можно и калькулятором.А если не говорить детям, что можно на калькуляторе, а пусть в уме считают? Что-то мне подсказывает, что сосчитают:)

Научился человек мало-мальски складывать числа в пределах ста. Не надо дрючить его до стопроцентной решаемости подобных примеров. Переходите к более сложным. Там ему это сложение точно понадобится, как простейшее действие. И натренируется.

Я сначала сидел, смотрел, как он считает, называет мне ответ, а я говорил, правильно, или нет. Теперь ухожу. Пусть сам пишет ответ на доску. Приду – проверю. Так появляется малюсенькая пока ответственность за свои расчёты. Нужно же принять своё решение, какой ответ написать.Разработали систему поощрений. Даю десять примеров на доске. Решил пример правильно, получаешь +1, а если неправильно, то получаешь –1.

ЗадачкиЦифры складывать хорошо! А как на счёт прикладного счёта? У Паши было пять яблок, два он потерял… Нужны задачи, чтоб ребёнок сам вычленил важное. Задачи нашёл в сети

И много интересных тестов. Очень приятно узнать, что мой сын в пять лет получает пятёрку по математике за первый класс.А ведь ещё надо прочитать условие задачи, вникнуть и потом только решать. Так ещё и чтение потренировали.

УчебникиЕсли вы занимаетесь с ребёнком математикой, сверяйтесь со школьными учебниками. Там есть много мелочей, которые кажутся сами собой разумеющимися, например, измерение длин линейкой. Незнание таких мелочей, не будь они разобраны с ребёнком, могут неожиданно всплыть, и напомнить вам о том, что учебники писались отнюдь не зря.Глупость какая-то с современными учебниками по математике. Во-первых, их слишком много. Во-вторых, зачем-то они в двух-трёх томах на учебный год. В-третьих – их невозможно понять. Мне, взрослому человеку с двумя высшими образованиями непонятны элементарные вещи: нарисованы черепахи и листья, а на следующей картинке черепах стало меньше, а листья стали зачёркнутыми. Никаким понятным мне способом я не могу объяснить, что произошло между этими картинками. Сын тоже ответа не дал.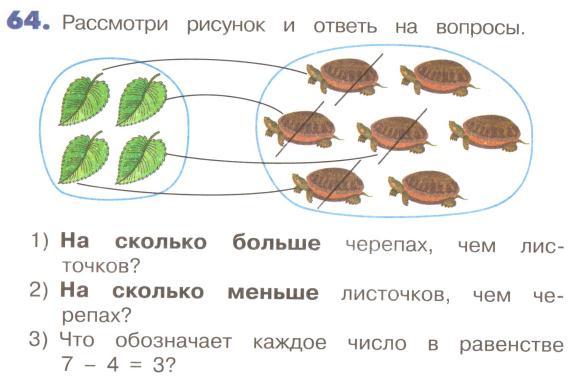Достали через тёщу учебник 1988 года. Вот это класс! Он на весь год, а размером с один из современных томов. Картинки в нём живые и интуитивно понятные. Ощущается течение учебного года: вот первое сентября, вот годовщина Революции, Новый год, 23 февраля, 8 марта, Первомай, День Победы. Конечно, педагогу к этому учебнику обязательно полагается хрестоматия. Её я не нашёл, но, сдаётся мне, советский вариант и тут выиграет у современных.

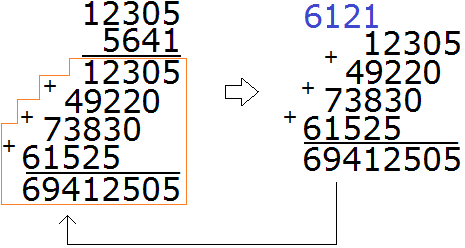
Складываем, вычитаем столбиком десятизначные числа. Сыну чуть больше 5 лет.Скоро будем умножать.