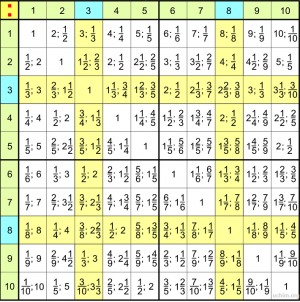
Таблица умножения для детей

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.Давайте рассмотрим задачи на умножение уровня второго класса:

1. Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

2. В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

3. Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

4. В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

5. Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

6. В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

7. Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

8. В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра «Числовой охват»

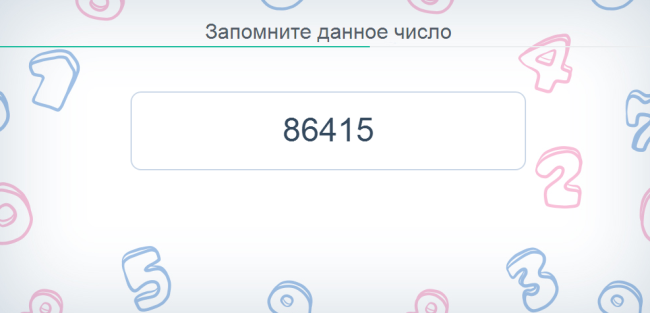
Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Математические сравнения»

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Умножение на 10, 100, 1000

Чтобы умножить любое число на 10,  100 или 1000, достаточно дописáть к множимому количество нулей из множителя.

Например, чтобы умножить 12 на 10, нужно к множимому 12 дописать в конце ноль из множителя 10. В результате получим ответ 120

Еще примеры:

12 × 100 = 1200 (к 12 дописали два нуля, поскольку в числе 100 два нуля)

12 × 1000 = 12000 (к 12 дописали три нуля, поскольку в числе 1000 три нуля)

15 × 100 = 1500 (к 15 дописали два нуля, поскольку в числе 100 два нуля)

320 × 100 = 32000 (к 320 дописали два нуля, поскольку в 100 два нуля)

Если нулём оканчивается не множитель, а множимое, то для получения ответа нужно дописать ноль после множителя.

Например, чтобы умножить 10 на 12, нужно в ответе записать множитель 12 и дописать в конце один ноль:

10 × 12 = 120

Умножение 3 класс

В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление.

Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.

Умножение столбиком:

Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.

1 шаг. Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг. Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.

Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг. Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг. Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.

Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!

5 шаг. Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг. Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

     1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

     2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

     3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

     4. Многоэтажные дробные выражения  приводим в вид обыкновенных, пользуясь делением через 2 точки.

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Умножение чисел, которые оканчиваются нулями

Если оба числа оканчиваются нулями, то нужно перемнóжить те цифры, которые нулями не являются, затем к полученному результату дописáть все нули из обоих чисел.

Например, умнóжим 20 на 30.

20 × 30

Видим, что оба числá содержат по нулю. Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 2 и 3. Два умножить на три будет шесть:

20 × 30 = 6

Теперь к полученному результату, то есть к числу 6 дописываем все нули из обоих чисел. В числе 20 один ноль, в числе 30 также один ноль. Итого два нуля. Дописываем два нуля к числу 6

20 × 30 = 600

Пример 2. Умножить 40 на 300

Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 4 и 3. Четыре умножить на три будет двенадцать:

40 × 300 = 12

Теперь к полученному результату, то есть к числу 12 дописываем все нули из обоих чисел. В числе 40 один ноль, в числе 300 — два нуля. Итого три нуля. Дописываем три нуля к числу 12

40 × 300 = 12000

Пример 3. Умножить 600 на 3000

Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 6 и 3. Шесть умножить на три будет восемнадцать:

600 × 3000 = 18

Теперь к полученному результату, то есть к числу 18 дописываем все нули из обоих чисел. В числе 600 два нуля, в числе 3000 — три нуля. Итого пять нулей. Дописываем пять нулей к числу 18

600 × 3000 = 1800000

Умножение многозначных чисел на многозначные

Умножение многозначных чисел на многозначные происходит таким же образом, как и умножение многозначных на однозначные. Каждая цифра многозначного числа умножается на каждую цифру другого многозначного числа. Единственное отличие заключается в том, что в конце образуется своего рода лесенка ответов, которые надо сложить. Рассмотрим несколько примеров, чтобы хорошо понять это.

Пример 1. Найти значение выражения 12 × 14

Записываем данное выражение в столбик — единицы под единицами, десятки десятками:

Теперь умножаем каждую цифру числа 12 на каждую цифру числа 14. Делать это надо по-очереди, начав с четвёрки. В результате таких действий мы приходим к умножению многозначного числа на однозначное, которое проходили ранее:

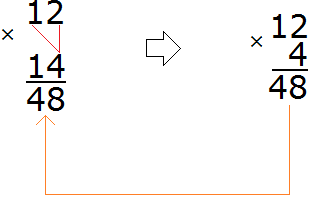
Умножив 12 на 4, мы получили число 48, которое записали таким образом, чтобы разряд единиц этого числа оказался под четверкой, на которую мы умножали число 12.

Теперь умножаем 12 на 1:

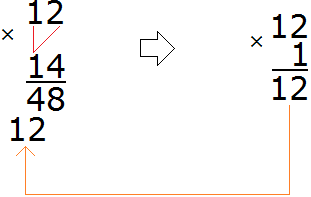
Умножив 12 на 1 мы получили число 12 и записали его таким образом, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножали число 12.

Мы получили лесенку ответов 48 и 12, которую надо сложить. Складываем и получаем ответ 168

В данном примере множитель 14 это четыре единицы и один десяток. Тогда умножение 12 на 14 можно понимать как увеличение числа 12 в четыре раза и в десять раз. Этим и объясняется появление лесенки в конце решения. Давайте посмотрим как это выглядит на каждом этапе:

Увеличим число 12 в четыре раза, получим число 48

Увеличим число 12 в десять раз, получим число 120. Записываем 120 так, чтобы можно было сложить единицы этого числа с единицами числа 48, а десятки числа 120 можно было сложить с десятками числа 48

Теперь сложим получившуюся лесенку ответов. Единицы сложим с единицами, десятки с десятками, сотни с сотнями. В результате образуется окончательный ответ:

Но чаще всего множитель не группируется с помощью разрядов, и умножение выполняют, умножая каждую цифру множимого на каждую цифру множителя.

Пример 2. Найти значение выражения 25 × 36

Записываем данное выражение в столбик

Умножаем каждую цифру числа 25 на каждую цифру числа 36.

Умножим 25 на 6:

Умножаем 25 на 3:

Теперь сложим получившуюся лесенку:

Получили ответ 900.

Рассмотрим большой и сложный пример на умножение: 12305 × 5641. Будем придерживаться ранее изученных правил.

Сначала записываем в столбик данное выражение

Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.

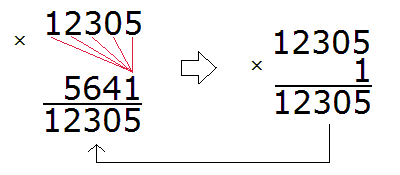
Умножив 12305 на 1, мы получили 12305 и записали это число так, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножили 12305.

Теперь умножаем 12305 на следующую цифру 4:

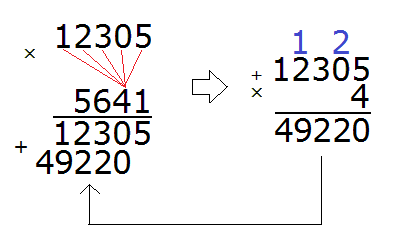Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.

Умножаем 12305 на следующую цифру 6:

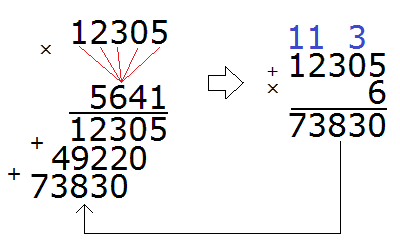
Умножив 12305 на 6, мы получили 73830 и записали это число так, чтобы разряд единиц этого числа оказался под шестёркой, на которую мы умножали 12305.

Теперь умножаем 12305 на последнюю цифру 5:

Умножив 12305 на 5, мы получили 61525 и записали это число так, чтобы разряд единиц этого числа оказался под пятёркой, на которую умножали 12305.

В результате мы получили большую лесенку, которую надо сложить. Складываем:

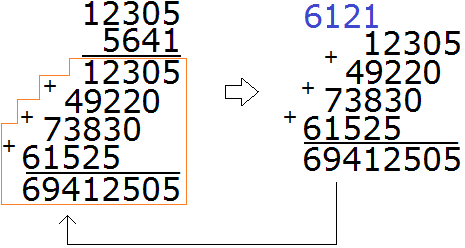
Получили окончательный ответ 69412505.

Если вы поняли этот пример, то можно сказать, что умножение больших чисел вы усвоили на отлично.

На этом урок по умножению можно завершить. Обязательно потренируйтесь, решив несколько примеров, которые даны ниже.

Важно отметить, что все эти стрелки и подробные решения, как на картинках в «боевых условиях» рисовать не принято. Нужно уметь сразу записывать ответы, выполняя в уме все вычисления

Исключением является то, если человек давно не занимался математикой или никогда ею не занимался. В таком случае можно рисовать для себя стрелки и другие вспомогательные схемы для хорошего усвоения материала.

Умножение многозначного числа на однозначное

Чтобы умножить многозначное число на однозначное, надо умножить каждую цифру многозначного числа на это однозначное число. Например, найдем значение выражения 12 × 3. Записываем данное выражение в столбик, при этом единицы должны быть под единицами. Всё это соединяется знаком умножения ( × )

Далее каждая цифра многозначного числа умножается на 3. Умножать начинаем с разряда единиц, то есть с цифры 2. Два умножить на три будет шесть. Записываем цифру 6 в разряде единиц нашего ответа:

Теперь умножаем 1 на 3, получаем 3. Записываем цифру 3 в разряде десятков нашего ответа:

Получили ответ 36.

В данном примере множимым было число 12, а множителем число 3. Число 12 это две единицы и один десяток. Наша задача заключалась в том, чтобы увеличить эти две единицы и один десяток в 3 раза. Тогда решая этот пример, можно было бы рассуждать следующим образом:

Увеличим две единицы в 3 раза: 2 × 3 = 6. Получили шесть единиц. Записываем цифру 6 в разряде единиц нового числа

Увеличим один десяток в 3 раза: 1 × 3 = 3. Получили три десятка. Записываем цифру 3 в разряде десятков нового числа:

Иногда при умножении одной цифры многозначного числа на однозначное число получается многозначное число. В этом случае сначала записывается одна цифра из разряда единиц, а остальные цифры переносятся на следующий разряд, к которому они будут добавлены после вычисления.

Например, найдем значение выражения 23 × 6

Умножаем каждую цифру числа 23 на 6. Начинаем с тройки: 3 × 6 = 18. Восемнадцать не вмещается в разряд единиц нашего ответа, поэтому сначала записывается 8, а 1 переносится на следующий разряд. Эта единица будет прибавлена к результату умножения 2 на 6

Теперь умножаем 2 на 6, получаем 12, плюс единица, которая досталась от предыдущего умножения. На рисунке эта единица выделена синим цветом. Вычисляем (2 × 6) + 1 = 13

Получили ответ 138. В данном примере множимым было число 23, а множителем число 6. Число 23 это три единицы и два десятка. Наша задача заключалась в том, чтобы увеличить эти три единицы и два десятка в 6 раз. Тогда решая этот пример, можно было бы рассуждать следующим образом:

Увеличим три единицы в 6 раз: 3 × 6 = 18. Получили восемнадцать единиц. Произошло переполнение разряда в разряде единиц. Число 18 это 8 единиц и 1 десяток. 8 единиц записываем в разряде единиц нового числа, а 1 десяток отправляем к разряду десятков. Этот десяток мы прибавим, когда увеличим два десятка в шесть раз:

Увеличим два десятка в 6 раз: 2 × 6 = 12. Получили двенадцать десятков. Плюс прибавляем один десяток, который остался от числа 18.

12 десятков плюс 1 десяток будет 13 десятков. Записываем число 13 в разряде десятков нового числа, образуя окончательный ответ:

Пример 3. Найти значение выражения 326 × 5

Записываем в столбик данное выражение:

Умножаем каждую цифру числа 326 на 5. Начинаем с шестёрки: 6 × 5 = 30. Число 30 не вмещается в разряд единиц нашего ответа, поэтому сначала записываем 0, а тройку переносим на следующий разряд:

Теперь умножаем 2 на 5, получаем 10 плюс тройка, которая досталась от предыдущей операции: (2 × 5) + 3 = 13. Получили число 13, которое не вмещается в разряд десятков нашего ответа. Поэтому записываем сначала 3, а единицу переносим на следующий разряд:

Теперь умножаем последнюю тройку на 5, плюс прибавляем единицу, которая досталась от предыдущей операции: (3 × 5) + 1 = 16. Получили 16. Записываем это число целиком, образуя окончательный ответ:

Сокращенное умножение

Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:

Формулы сокращенного умножения

Пусть a, b принадлежат R, тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a+b)^2 = a^2 + 2ab + b^2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a-b)^2 = a^2 — 2ab + b^2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Формула: a^2 — b^2 = (a — b)(a + b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. Формула: (a + b)^3 = a^3 + 3a(^2)b + 3ab^2 + b^3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. Формула: (a-b)^3 = a^3 — 3a(^2)b + 3ab^2 — b^3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 + b^3 = (a + b)(a^2 — ab + b^2)

7. Разность кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 — b^3 = (a — b)(a^2 + ab + b^2)

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.