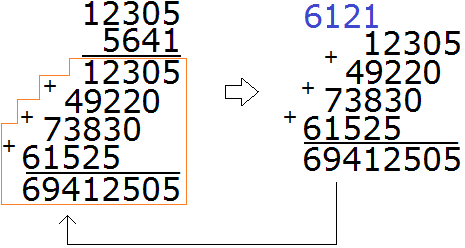
Таблица умножения и игра, чтобы быстро выучить

Классы математик (разряды и классы)

Чтобы детям было проще ориентироваться в числах, да и не только детям, было придумано разделение числа на классы и разряды.

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Такое разделение действительно очень удобно и легко запоминается. Гораздо проще в ходе обучения детей математике, рассказывая о какой-нибудь операции, говорить, как складывать столбиком, например. Потому что в ходе рассказа можно называть числа по разрядам и классам и так будет намного понятнее ученику, нежели просто называть цифрой.

Задание 2:

Сложная задача по математике для 4 класса: Из двух городов по реке одновременно выплыли навстречу друг другу две моторные лодки. Скорость первой лодки 15км/ч, второй лодки 35км/ч. Первая лодка двигалась по течению реки. Скорость течения реки 5км/ч. Через сколько часов лодки встретились, если расстояние между городами 250км?

Решение:

Пусть до встречи лодок первая проплыла x км. Тогда вторая лодка проплыла (250 — x) км. Учитывая скорость течения реки, скорость первой лодки 15 + 5 = 20км/ч. Соответственно, скорость второй лодки 35 — 5 = 30км/ч. Очевидно, что время в пути до встречи одинаково, поэтому можно записать уравнение: x/20 = (250 — x)/30; x * 30 = 20 * (250 — x); 30x = 5000 — 20x; 50x = 5000; x = 100км.

Первая лодка до встречи со второй прошла 100км. Рассчитаем время: t = x/20 = 100/20 = 5ч.

Для проверки мы можем рассчитать время второй лодки: t = x/20 = (250 — x)/30 = 150/30 = 5ч. Ответ: лодки встретились через 5 часов.

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг. Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг. Ставим точку под делителем.

5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Как отличить?

Предложение сложное и простое имеет тесную связь с количеством грамматических основ.

Чтобы понять, когда предложение простое, а когда сложное, нужно посчитать количество грамматических основ, что значит: те, кто говорит на русском языке, должны уметь правильно определять грамматические основы предложений. Без умения находить грамматическую основу предложения невозможно определить, простым или сложным является то или иное предложение.

Необходимо отличать самостоятельную грамматическую основу и однородные подлежащие или сказуемые. Также нужно понимать, что грамматической основой может быть и только подлежащее или только сказуемое.

Сравним простые предложения и сложные предложения.

Примеры простых предложения:

• Мы катались на аттракционах (1 грамматическая основа: мы катались).
• Я уехал к бабушке на каникулы (1 грамматическая основа: я уехал).
• Он открыл дверь и увидел меня (1 грамматическая основа с однородными сказуемыми: он открыл и увидел).

Примеры сложных предложений:

• Наступили холода, ребята надели теплые свитера (2 грамматические основы: холода наступили; ребята надели).
• Я вышел из школы, но мама еще не подошла (2 грамматические основы: я вышел; мама не подошла).
• Мой друг пришел, когда закончился дождь (2 грамматические основы: друг пришел; дождь закончился).

Что мы узнали?

Простое предложение – предложение с одной грамматической основой Сложное предложение – предложение с двумя и более грамматическими основами. В состав сложного предложения входят простые предложения, которые связаны по смыслу и интонационно. Между частями сложных предложений могут стоять союзы. Разграничение простого предложения от сложного предложения происходит по количеству грамматических основ.

Примеры для устного счёта 4 класс

Счёт в уме

Как тренировать навыки устного счёта, применяя наши примеры?

Практического материала для тренировки счёта в уме в интернете предостаточно. Наши примеры многоразового использования. Каждый пример включает все арифметические действия. Поэтому они наиболее применимы начиная с четвёртого класса. Счёт в пределах сотни. В примерах не действуют математические правила, где первыми надо выполнить умножение и деление, а также действия в скобках.

В каждом примере пять действий, выполняющихся последовательно. Ещё раз – последовательно друг за другом. Например, в выражении 3х7+69-65:5 как идут действия друг за другом, так их и надо выполнять

Вашему ученику трудно выполнить все пять действий? Начинайте с одного. Решите в уме первое действие всех примеров. Потом первые два, три. По мере формирования навыка устного счёта добавляйте по одному действию, и так до пяти. К следующему этапу переходите после качественного освоения предыдущего.

Иногда задают вопрос: а не запомнит ребёнок результаты вычислений? В нашей практике такого не случалось, каждый решался как новый. Примеры разнообразны, действия тоже в разной последовательности.

Тренироваться надо ежедневно по 3-5 минут. Только в этом случае будет результат. Взрослый читает задание, ребёнок старается удержать в памяти на время счёта. Забыл, подскажите. Но не давайте список примеров в руки. Это уже не будет устный счёт.

Соблюдайте технику безопасности. Не заставляйте ребёнка перенапрягаться, работая больше 5 минут. Начало любой тренировки, особенно умственной, требует больших энергетических затрат.

Устойчивый навык устных вычислений у разных ребят требует разного времени для формирования. Следует это помнить.

Математика 1 класс

В первом классе проходят раздел математики — арифметику. Арифметика – раздел математики, работающий с числами и вычислениями (действиями с числами).

В первом классе, как правило, проходят первые две самые простые операции с числами: сложение, вычитание.

Сложение – это арифметическое действие, в процессе которого складываются два числа, а их результатом будет новое – третье.

Формула сложения выражается так: a + b = c.

Вычитание – это арифметическое действие, в процессе которого из первого числа вычитается второе число, а итогом будет третье.

Формула сложения выражается так: a — b = c.

Операции производятся с однозначными цифрами. Редко встречаются двузначные. Потому что нужно, чтобы дети освоились, поняли технику.

Математика 6 класс

В 6ом классе появляется тема преобразования дробей в строчную запись. Что это значит? Например, дана дробь ½, она будет равна 0,5. ¼ = 0.25.

Примеры могут составляться в таком стиле: 0.25+0.73+12/31.

Примеры для тренировки:

Задание №1:

Задание №2:

Задание №3:

1. В двух классах в общем было 92 стула. Из первого класса перенесли 16 стульев во второй класс и потом количество их уровнялось. Сколько стульев было в первом и втором классе изначально?

2. В двух ящиках лежало 240 кг яблок. Из второго ящика в первый переложили 18 кг яблок. После количество яблок в первом и втором ящике уровнялось. Сколько килограмм яблок было изначально в первом и втором ящике.

3. Автомобилист выехал из города в деревню со скоростью равно 11,5 км/ч. Спустя 2,4 часа оттуда же и в том же направлении выехал автобус со скоростью 46 км/ч. Спустя какое время автобус догонит автомобиль?

Сложное предложение

Сложное предложение – это предложение с двумя и более грамматическими основами.

В состав сложного предложения входят простые предложения. Простые предложения, находящиеся в составе сложного предложения, связаны друг с другом по смыслу и интонационно.

Части сложного предложения дополняют друг друга, превращают разную информацию в одну, более полную.

Чаще всего между частями сложного предложения ставятся запятые.

Между частями сложного предложения могут стоять союзы, но они могут и отсутствовать. Если союзов между частями сложного предложения нет, то это бессоюзное сложное предложение; союзные сложные предложения делятся на сложносочиненные (с сочинительными союзами) и сложноподчиненные (с подчинительными союзами).

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

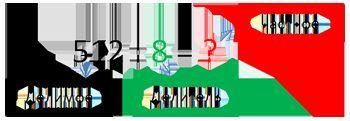
Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Математические матрицы»

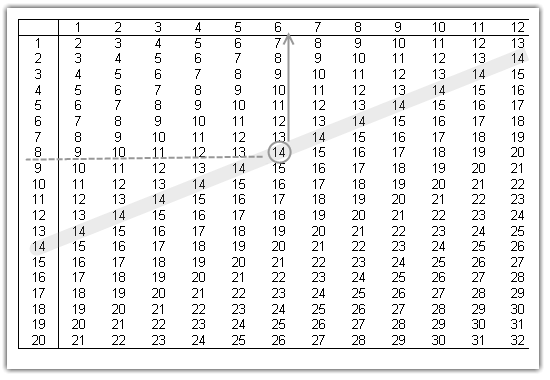
«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет:

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

1. Найти сумму цифр делимого.

2. Поделить на 3 или 9 (в зависимости от того, что вам нужно).

3. Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.