Математические головоломки для детей и взрослых

Загадки с подвохом

Задача 7. Отгадайте, кому принадлежит кукла: у Леры и Рады куклы с голубыми волосами, а у Дины и Стаси – со светлыми. У Рады и Стаси куклы в платьях, а у Леры и Дины – в юбках и блузах.

Определите хозяйку каждой куклы.

Задача 8. Хитрая загадка: есть подвал, в котором находятся 3 лампочки. Выключатели от этих лампочек находятся вне подвала так, что даже при открытых дверях в подвал не видно, горят ли лампочки. Как, войдя всего 1 раз в подвал, определить, который из 3-х выключателей какой лампочке соответствует?

Задача 9. Математическая загадка: у Кристины есть 4 разных платья и 3 разных пары туфель. Она собирается на вечеринку и думает, что ей надеть. Сколько у Кристины вариантов образа?

1) Метод графов.

Даны отношения между предметами и следуя по цепочке этих отношений, мы приходим к правильному результату. Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками. Рассмотрим метод графов на примере решения задачи.Задача “Любимые мультфильмы”: Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?Решение.Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками.
Поэтому граф на рисунке будет выглядеть следующим образом:

Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. Заметим, что по условию задачи у человека только один любимый мультфильм. Поэтому нужно найти единственно возможное соответствие между элементами двух множеств.

Правилоесли какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной.
Поэтому граф на рисунке будет выглядеть следующим образом:

Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри».

Задача решена.2) Круги Эйлера. Второй способ, которым решаются такие задачи круги Эйлера – задачи на пересечение или объединение множеств.Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

Загадки и задачи

Задания, которые побуждают детей мыслить логически, довольно разнообразны. С помощью упражнений, подходящих для детей 6-7 лет, можно:

• научить детей анализировать и сравнивать предметы, систематизировать их, находить закономерности;
• приучить к работе с рисунками и схемами;
• развивать речь;
• освоить порядковый и количественный счет;
• дать понимание взаимосвязей природных явлений.

Для развития логики полезно много беседовать и обсуждать, создавать что-то своими руками. Значительное место отводится и работе с наглядными пособиями – рисунками, книжками, распечатками, раскрасками, фото, разнообразными игрушками.

В 6 и 7 лет уже можно активно использовать математические задачи. К примеру, считать лапы у животных, фрукты или овощи на столе. Много заданий можно придумать с геометрическими фигурами, например, сортировать их по форме или размеру. Существует также немало упражнений с использованием картинок. К примеру, ребенку предлагают несколько карточек с изображениями предметов, а он должен выбрать, какие из них опасны, съедобны, могут двигаться.

Рассмотрим несколько интересных загадок.

• У Антона большое кислое яблоко, у Ани – большое сладкое. Чем они похожи, а что разное?
• Света и Оля рассматривали картинки в журнале и в книге. Где рассматривала картинки Света, если это не книга?
• У Даши есть 3 пары носков. Сколько всего у нее носков?
• На площадке играли 5 детей. Двое ушли домой, а потом вернулись. Сколько теперь детей на площадке?
• Маша взяла 3 конфеты, а Саша – на 1 больше. Сколько конфет съест Саша?
• По двору ходят утки. Ваня насчитал у них 8 ног. Сколько всего уток?
• В коробке лежит 7 машинок. Сколько мне нужно забрать, чтобы там осталось 3 машинки?
• На дереве висит 6 груш. Дети сорвали по одной, и на дереве осталось 2 груши. Сколько было детей?
• В плитке шоколада есть 6 долек. Сколько раз ее надо разломать, чтобы поделить всю плитку на отдельные дольки?
• Денис принес 3 кубика, а Максим – 4. Сколько кубиков будет в башне, которую вместе построят ребята?
• В кошельке есть деньги, на которые можно купить 2 пачки печенья или 1 коробку конфет. Что стоит дороже?
• На двух полках стоит одинаковое количество книг. С одной забрали 2 книги и поставили на вторую. Сколько книг стало на каждой полке?
• В тарелке лежат 3 апельсина, а в коробке – вдвое больше. Сколько апельсинов находится в коробке?
• Торт разрезали на половины, а потом каждую из них – на 3 части. Сколько кусков получилось?
• Диме 10 лет, Маша на 5 лет младше. Сколько лет Маше?
• Мама испекла к завтраку 12 кексов. Все съели, кроме двух. Сколько осталось?
• На столе лежало 3 яблока. Одно разрезали на половинки. Сколько яблок на столе теперь?

Логические игры для детей

Игры для ребенка 6-7 лет для развития логики можно поделить на такие группы:

1. Графические. Игры данного вида рассчитаны на усовершенствование мелкой моторики у детей и приспособление детских рук к письму. К таким занятиям относятся упражнения рисования по клеткам, разукрашивание изображений с обозначенными цветами, соединение рисунка по точкам.

2. Математические головоломки. Основой таких игр является обучение детей устно считать, постигать азы логики и творческого мышления.

3. Словесные. Целью таких игр является улучшение речевого инструмента детей, обогащение тезауруса, это приводит к четкости и чистоте слов. Дети учатся воспринимать информацию на слух. Например: учитель говорит два слова (вишня и слива), ученик должен уметь словесно выразить их различия между собой.

4. Игровая литература. Замечательный метод для того, что бы привить любовь к чтению и научить познавать окружающую среду с помощью книг, а также игры способствуют развитию памяти и внимания. Сегодня, магазины предлагают огромный выбор книг, которые помогут в развитии детской логики, но лучше всего ориентироваться на такие книги: Мальцева И.В. «Логика для дошкольников» и рабочую тетрадь Бортниковой Е

«Развиваем внимание и логическое мышление»

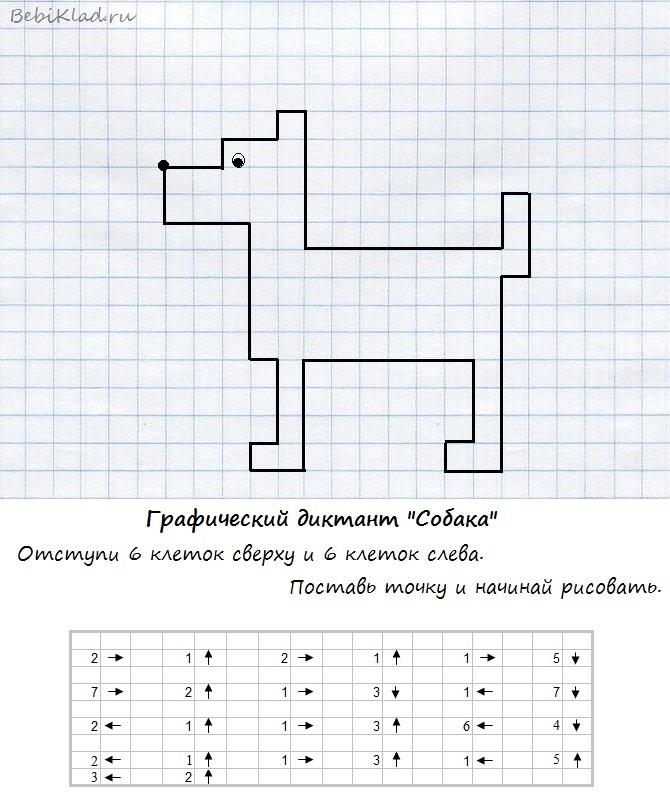
Логическая игра «Домашний диктант»

Цель: улучшение мелкой моторики, восприимчивости информации на слух.

Материалы: листок бумаги в клетку (желательно покрупнее), цветные карандаши.

Взрослый должен продиктовать ребенку действия. Например: три клетки произвольно, вертикально, пять клеток, начиная со второй из трех вправо, одну клетку от первой из пяти вверх. Потом попросить маленького участника разукрасить, полученную фигуру. Другие графические диктанты смотрите здесь.

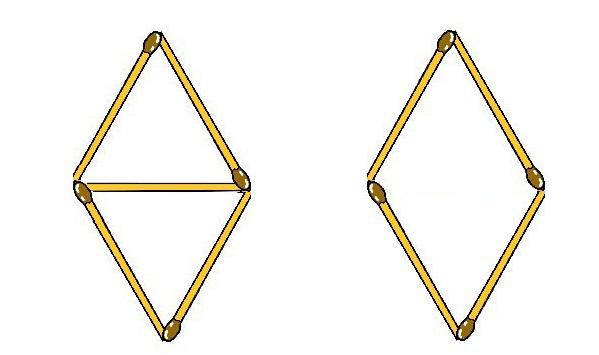
Логическая игра «Треугольники»

Цель: обучение счету и нестандартному мышлению.

Материалы: 5 спичек.

Взрослый просит ребенка из пяти спичек (зубочисток, палочек от мороженого) сложить два треугольника, если у участника игры это получилось, то попросить убрать одну спичку так, чтобы получился ромб.

Логическая игра «Сделай рассказ»

Цель: развитие умений непрерывной беседы, улучшение словарного запаса.

Материалы: картинки, которые вместе составляют собой единый рассказ. Например: первая картинка – девочка, вторая картинка – эта же девочка идет, третья картинка – эта же девочка стоит около магазина. Можете распечатать и нарезать карточки с персонажами с картинки ниже.

Взрослый должен разложить перед ребенком картинки и попросить рассказать ему о том, что происходит на них, но только в форме непрерывного рассказа.

Логическая игра «Противоположности»

Цель: развитие словарного запаса и умение находить различия.

Материалы: не нужны.

Взрослый говорит слова, а он ищет противоположное значение. Например: белый – черный, грустный – веселый, мокрый – сухой.

Логическая игра «Дерево»

Цель: развить умение логической мысли и чувства последовательности.

Материалы: четыре картинки, отражающие стадии деревьев (первая – деревья с почками (первыми листочками), вторая – цветущие деревья, третья – деревья с плодами, четвертая – пожелтевшие (опавшие) листья).

Взрослый раскладывает их в разном порядке, который не соответствует правильной последовательности и просит ребенка сложить их так, чтобы последовательность развитие деревьев не нарушалась.

Как рассадить интровертов в баре

А вот задач­ка на струк­ту­ры дан­ных, сор­ти­ров­ку и алго­рит­ми­ку, кото­рая воз­мож­на толь­ко в нашей стране.

В Петер­бур­ге на ули­це Рубин­штей­на есть один бар, в кото­рый ходят лишь необ­щи­тель­ные люди, назо­вём их интро­вер­та­ми. (На самом деле интро­вер­ты общи­тель­ные, необ­щи­тель­ность — это миф. Но это задач­ка, поэто­му упро­стим.)

Интро­вер­ты садят­ся вдоль бар­ной стой­ки, где есть 25 мест. Когда вхо­дит новый посе­ти­тель, он все­гда садит­ся у стой­ки как мож­но даль­ше от осталь­ных гостей. Никто не садит­ся на сосед­нее место рядом с дру­гим интро­вер­том: если кто-то вхо­дит и видит, что сво­бод­ных мест мало и надо сесть рядом с кем-то, то он ухо­дит.

Бар­мен хочет полу­чить как мож­но боль­ше кли­ен­тов. У него есть пра­во поса­дить само­го пер­во­го посе­ти­те­ля на любое место у стой­ки. Куда выгод­нее поса­дить пер­во­го интро­вер­та с точ­ки зре­ния бар­ме­на?

Решение

Для нача­ла най­дём иде­аль­ный вари­ант, кото­рый устро­ил бы бар­ме­на. Для это­го нари­су­ем 25 квад­ра­тов в ряд и закра­сим те, на кото­рых кто-то сидит. Помни­те, что ни один интро­верт по зада­че не сядет на сосед­нее место к дру­го­му.

Полу­ча­ет­ся, что это самая плот­ная рас­сад­ка, кото­рая воз­мож­на в этом баре. Так у стой­ки сидят 13 чело­век. Оста­лось толь­ко най­ти место для само­го пер­во­го посе­ти­те­ля.

Для нача­ла попро­бу­ем решить эту зада­чу в лоб и поса­дим пер­во­го посе­ти­те­ля на пер­вый стул:

Теперь вто­рой посе­ти­тель дол­жен сесть на сво­бод­ное место как мож­но даль­ше от него, то есть занять стул № 25:

Тре­тье­му доста­ёт­ся стул № 13, так как он ров­но посе­ре­дине меж­ду эти­ми дву­мя:

Два сле­ду­ю­щих зай­мут сво­бод­ные места точ­но посе­ре­дине меж­ду цен­траль­ным и боко­вы­ми:

И вот тут наста­ёт момент исти­ны: четы­ре сле­ду­ю­щих посе­ти­те­ля тоже сядут точ­но посе­ре­дине меж­ду заня­ты­ми места­ми. Это зна­чит, что меж­ду каж­дым будет по 2 пустых места:

В ито­ге у нас заня­то все­го 9 мест, но сесть боль­ше нику­да нель­зя: у каж­до­го сво­бод­но­го сту­ла есть как мини­мум один заня­тый сосед. Зна­чит, этот вари­ант не под­хо­дит. Нужен дру­гой.

Что­бы прий­ти к пра­виль­но­му отве­ту, попро­бу­ем решать зада­чу с кон­ца.

Вспом­ним иде­аль­ную рас­сад­ку:

Здесь сидит мак­си­маль­ное коли­че­ство гостей — 13, и меж­ду каж­дым из них есть сво­бод­ное место. Отмо­та­ем на шаг назад и посмот­рим, как мог­ли бы сидеть интро­вер­ты, что­бы новые гости сели точ­но меж­ду ними:

В этом слу­чае 6 новых гостей садят­ся точ­но посе­ре­дине меж­ду заня­ты­ми сту­лья­ми и иде­аль­но запол­ня­ют все места.

Теперь сде­ла­ем ещё шаг назад и посмот­рим, как долж­ны сидеть гости, что­бы новые кли­ен­ты сели на нуж­ные сту­лья:

Полу­ча­ет­ся, что если мы поса­дим пер­вых четы­рёх гостей так, как на рисун­ке выше, то даль­ше всё будет хоро­шо. Сде­ла­ем ещё шаг назад, что­бы понять, как они смог­ли так сесть:

Из рисун­ка вид­но, что два новых посе­ти­те­ля долж­ны сесть как мож­но даль­ше от заня­тых мест. Для это­го один садит­ся ров­но посе­ре­дине меж­ду дву­мя заня­ты­ми, а вто­рой — с само­го края, на пер­вое место. Таким обра­зом, меж­ду все­ми ними будет мак­си­маль­но воз­мож­ное рас­сто­я­ние. Оста­лось понять, как сели эти пер­вые два интро­вер­та.

Если бы пер­вый гость сел с краю на стул № 25, вто­ро­му бы при­шлось сесть с про­ти­во­по­лож­но­го края на стул № 1 (мы это разо­бра­ли в самом нача­ле, в непра­виль­ном вари­ан­те). Зна­чит, пер­вый гость сел на стул № 9, а вто­ро­му при­шлось сесть мак­си­маль­но дале­ко от него — на самый послед­ний стул:

Полу­ча­ет­ся, само­го пер­во­го гостя бар­мен дол­жен поса­дить на стул № 9.

Как так вышло? Про­сто посчи­та­ли от обрат­но­го. Про­грам­ми­сты назы­ва­ют это Test-First Development, хех.

Загадки с подвохом для детей

Начнем с малого и решим 5 загадок для самых маленьких. Взрослым ответ покажется очевидным, а вот ребятам придется подумать (но может быть и наоборот). Чур, не подсказывать!

Загадка №1.
Что ты никогда не сможешь съесть на завтрак?
Ответ: Обед и/или ужин.

Загадка №2.
Что может путешествовать по свету, оставаясь в одном и том же углу?
Ответ: Почтовая марка.

Загадка №3.
В одноэтажном розовом доме жил розовый человек, розовый кот, розовая рыбка, был розовый компьютер, розовое кресло, розовый стол, розовый телефон, розовая душевая кабина – все было розовым! Какого цвета была лестница?
Ответ: В этом доме не было лестницы, потому что это был одноэтажный дом.

Загадка №4.
Что настолько же огромное, как слон, но ничего не весит?
Ответ: Тень слона.

Загадка №5.
Какое слово в словаре написано неправильно?
Ответ: Это слово «неправильно».

Мы знаем, что вам и вашим детям, как минимум, было интересно. А как максимум – вы серьезно задумались и хотите идти дальше!